Microsoft ได้เปิดตัว rStar-Math ซึ่งเป็นความต่อเนื่องและการปรับปรุงจาก เฟรมเวิร์ก rStar เพื่อขยายขอบเขตของโมเดลภาษาขนาดเล็ก (SLM) ในการให้เหตุผลทางคณิตศาสตร์
rStar-Math ได้รับการออกแบบมาเพื่อแข่งขันกับระบบที่ใหญ่กว่า เช่น การแสดงตัวอย่าง o1 ของ OpenAI บรรลุเกณฑ์มาตรฐานที่น่าทึ่งในการแก้ปัญหา ในขณะเดียวกันก็แสดงให้เห็นว่าโมเดลขนาดกะทัดรัดสามารถทำงานได้ในระดับแข่งขันได้อย่างไร การพัฒนานี้แสดงให้เห็นถึงการเปลี่ยนแปลงในลำดับความสำคัญของ AI โดยเปลี่ยนจากการปรับขนาดเป็นการเพิ่มประสิทธิภาพสำหรับงานเฉพาะ
ก้าวจาก rStar ไปสู่ rStar-Math
The rStar กรอบการทำงานจากฤดูร้อนที่แล้วได้วางรากฐานสำหรับการปรับปรุงการใช้เหตุผล SLM ผ่าน Monte Carlo Tree Search (MCTS) ซึ่งเป็นอัลกอริทึมที่ปรับแต่งโซลูชันโดยการจำลองและตรวจสอบหลายเส้นทาง
rStar แสดงให้เห็นว่าโมเดลขนาดเล็กสามารถจัดการกับงานที่ซับซ้อนได้ แต่การใช้งานยังคงเป็นแบบทั่วไป. rStar-Math สร้างบนรากฐานนี้ด้วยนวัตกรรมที่ตรงเป้าหมายซึ่งออกแบบมาเพื่อการใช้เหตุผลทางคณิตศาสตร์โดยเฉพาะ
หัวใจสำคัญของความสำเร็จของ rStar-Math คือระเบียบวิธีห่วงโซ่แห่งความคิดด้วยโค้ดเสริม (CoT) ซึ่งแบบจำลองดังกล่าวสร้างโซลูชันในทั้งสองอย่าง ภาษาธรรมชาติและโค้ด Python ที่ปฏิบัติการได้
โครงสร้างเอาต์พุตคู่นี้ช่วยให้แน่ใจว่าขั้นตอนการให้เหตุผลระดับกลางสามารถตรวจสอบได้ ลดข้อผิดพลาด และรักษาความสอดคล้องทางตรรกะ นักวิจัยเน้นย้ำถึงความสำคัญของแนวทางนี้ โดยระบุว่า”ความสม่ำเสมอร่วมกันสะท้อนถึงการปฏิบัติของมนุษย์โดยทั่วไปโดยไม่มีการควบคุมดูแล โดยที่การตกลงร่วมกันระหว่างเพื่อนร่วมงานเกี่ยวกับคำตอบที่ได้รับบ่งชี้ถึงความเป็นไปได้ที่สูงขึ้นของความถูกต้อง”
ที่เกี่ยวข้อง: โมเดล DeepSeek R1-Lite-Preview ของจีนตั้งเป้าเป็นผู้นำของ OpenAI ในด้านการใช้เหตุผลอัตโนมัติ
นอกเหนือจาก CoT แล้ว rStar-Math ยังแนะนำโมเดลการตั้งค่ากระบวนการ (PPM) ซึ่งประเมินและจัดอันดับขั้นตอนระดับกลางโดยอิงจากคุณภาพ “PPM ใช้ประโยชน์จากข้อเท็จจริงที่ว่า แม้ว่าค่า Q ยังคงไม่แม่นยำเพียงพอที่จะให้คะแนนขั้นตอนการให้เหตุผลแต่ละขั้นตอน แม้ว่าจะใช้ MCTS อย่างกว้างขวาง แต่ค่า Q สามารถแยกแยะขั้นตอนเชิงบวก (ถูกต้อง) ได้อย่างน่าเชื่อถือจาก ค่าลบ (ไม่เกี่ยวข้อง/ไม่ถูกต้อง)
ดังนั้น วิธีการฝึกอบรมจึงสร้างคู่การตั้งค่าสำหรับแต่ละขั้นตอนตามค่า Q และใช้การสูญเสียการจัดอันดับแบบคู่เพื่อปรับการทำนายคะแนนของ PPM ให้เหมาะสมสำหรับขั้นตอนการให้เหตุผลแต่ละขั้นตอน เพื่อให้ได้การติดฉลากที่เชื่อถือได้ แนวทางนี้หลีกเลี่ยงวิธีการทั่วไปที่ใช้ค่า Q เป็นป้ายกำกับรางวัลโดยตรง ซึ่งโดยธรรมชาติแล้วจะส่งเสียงดังและไม่แม่นยำในการให้รางวัลแบบเป็นขั้นตอน”
สุดท้าย สูตรวิวัฒนาการตนเองสี่รอบที่สร้างทั้งขอบเขตอย่างก้าวหน้า รูปแบบนโยบายและ PPM ตั้งแต่เริ่มต้น
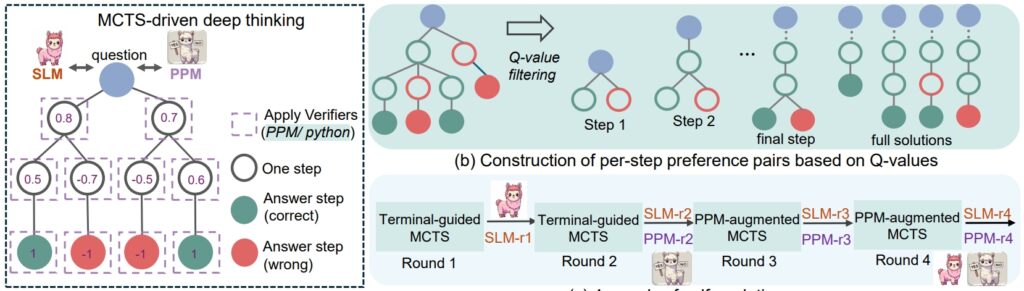ขั้นตอนการให้เหตุผล rSTar-Math (ที่มา: เอกสารวิจัย)
ประสิทธิภาพที่ท้าทายโมเดลขนาดใหญ่
rStar-Math กำหนดมาตรฐานใหม่ในการให้เหตุผลทางคณิตศาสตร์ การวัดประสิทธิภาพ การบรรลุผลลัพธ์ที่ทัดเทียมกัน และในบางกรณีก็เหนือกว่าระบบ AI ที่ใหญ่กว่า
บนชุดข้อมูล GSM8K เป็นการทดสอบการใช้เหตุผลทางคณิตศาสตร์ ความแม่นยำของแบบจำลอง 7 พันล้านพารามิเตอร์ดีขึ้นจาก 12.51% เป็น 63.91% หลังจากรวม rStar-Math ไว้ใน American Invitational Mathematics Examination (AIME) แบบจำลองนี้สามารถแก้ไขปัญหาได้ 53.3% ติดอันดับ 20% แรกของโรงเรียนมัธยมศึกษาตอนปลาย ผู้เข้าร่วม.
ผลลัพธ์ของชุดข้อมูล MATH ก็น่าประทับใจไม่แพ้กัน โดย rStar-Math มีอัตราความแม่นยำ 90% ซึ่งมีประสิทธิภาพเหนือกว่า o1-preview ของ OpenAI
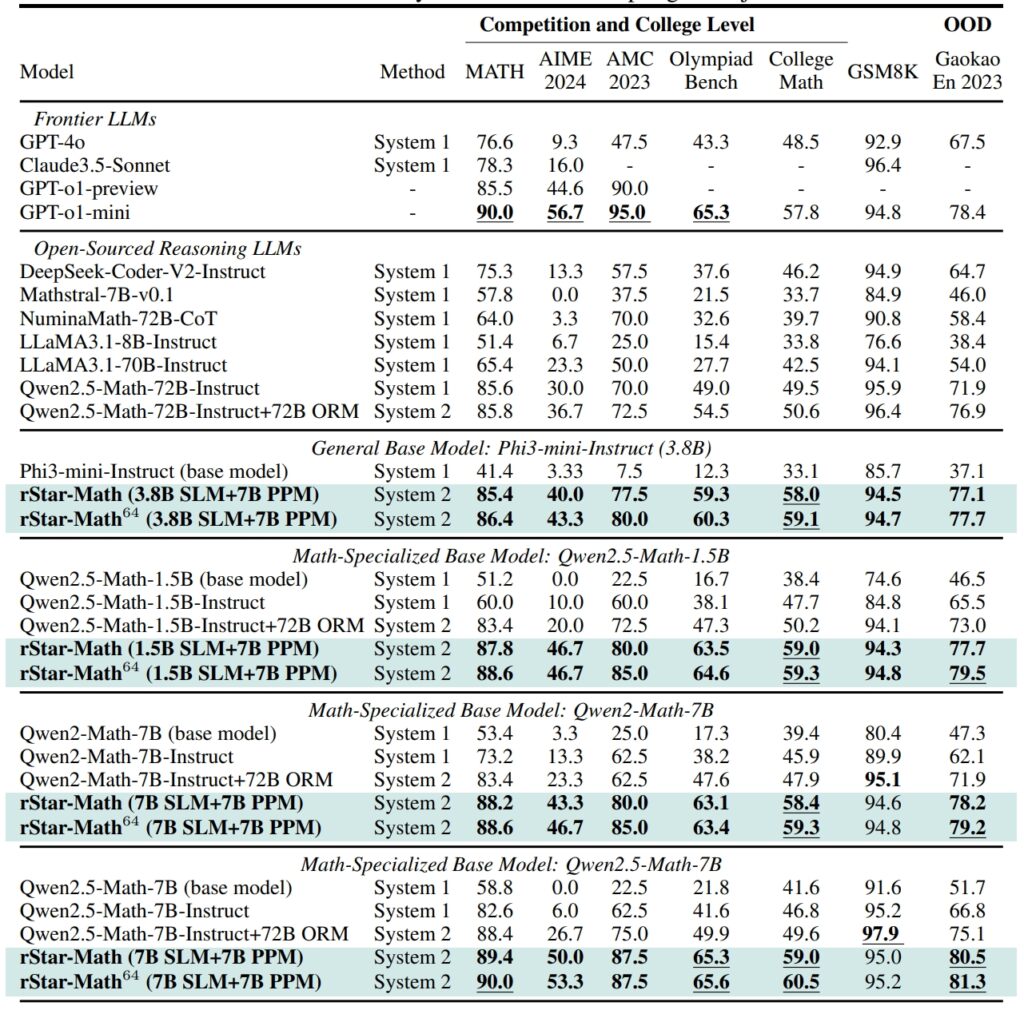ประสิทธิภาพของ rStar-Math และ LLM ระดับแนวหน้าอื่นๆ มากที่สุด เกณฑ์มาตรฐานทางคณิตศาสตร์ที่ท้าทาย (ที่มา: เอกสารการวิจัย)
ความสำเร็จเหล่านี้เน้นย้ำถึงความสามารถของกรอบงานในการทำให้ SLM สามารถจัดการกับงานที่ก่อนหน้านี้ถูกครอบงำโดยโมเดลขนาดใหญ่ที่ต้องใช้ทรัพยากรมาก ด้วยการเน้นความสอดคล้องเชิงตรรกะและขั้นตอนกลางที่ตรวจสอบได้ rStar-Math จัดการกับหนึ่งในความท้าทายที่ยังคงมีอยู่อย่างต่อเนื่องที่สุดของ AI นั่นคือ การรับรองการให้เหตุผลที่เชื่อถือได้ในพื้นที่ปัญหาที่ซับซ้อน
นวัตกรรมทางเทคนิคที่ขับเคลื่อน rStar-Math
วิวัฒนาการจาก rStar สู่ rStar-Math นำเสนอความก้าวหน้าที่สำคัญหลายประการ การบูรณาการ MCTS ยังคงเป็นศูนย์กลางของกรอบการทำงาน ทำให้แบบจำลองสามารถสำรวจเส้นทางการให้เหตุผลที่หลากหลาย และจัดลำดับความสำคัญของแนวทางที่มีแนวโน้มมากที่สุด
การเพิ่มการใช้เหตุผล CoT โดยมุ่งเน้นไปที่การตรวจสอบรหัส ช่วยให้มั่นใจได้ว่าผลลัพธ์สามารถตีความได้และแม่นยำ
ที่เกี่ยวข้อง: QwQ-32B ของ Alibaba-ดูตัวอย่างเข้าร่วมการต่อสู้การใช้เหตุผลโมเดล AI ด้วย OpenAI
บางทีการเปลี่ยนแปลงที่ยิ่งใหญ่ที่สุดอาจเป็นกระบวนการฝึกฝนที่พัฒนาตนเองของ rStar-Math กรอบการทำงานซ้ำสี่รอบจะปรับแต่งโมเดลนโยบายและ PPM โดยผสมผสานข้อมูลการให้เหตุผลที่มีคุณภาพสูงขึ้นในแต่ละขั้นตอน
วิธีการทำซ้ำนี้ทำให้แบบจำลองสามารถปรับปรุงประสิทธิภาพได้อย่างต่อเนื่อง โดยบรรลุผลลัพธ์ที่ล้ำสมัยโดยไม่ต้องพึ่งพาการกลั่นจากแบบจำลองที่ใหญ่กว่า
การเปรียบเทียบ rStar-Math ไปยัง o1 ของ OpenAI
ในขณะที่ Microsoft มุ่งเน้นไปที่การเพิ่มประสิทธิภาพโมเดลขนาดเล็ก OpenAI ยังคงให้ความสำคัญกับการขยายขนาดระบบของตน
o1 โหมด Pro ซึ่งเปิดตัวในเดือนธันวาคม 2024 โดยเป็นส่วนหนึ่งของแผน ChatGPT Pro มอบความสามารถในการให้เหตุผลขั้นสูงที่ปรับแต่งมาสำหรับการใช้งานที่มีความเสี่ยงสูง เช่น การเขียนโค้ดและการวิจัยทางวิทยาศาสตร์ OpenAI รายงานว่า o1 Pro Mode ได้รับอัตราความแม่นยำ 86% บน AIME และอัตราความสำเร็จ 90% ในเกณฑ์มาตรฐานการเข้ารหัส เช่น Codeforces
rStar-Math แสดงให้เห็นถึงการเปลี่ยนแปลงในนวัตกรรม AI ซึ่งท้าทายการมุ่งเน้นของอุตสาหกรรมไปที่โมเดลที่ใหญ่ขึ้น เป็นวิธีหลักในการบรรลุการใช้เหตุผลขั้นสูง ด้วยการปรับปรุง SLM ด้วยการเพิ่มประสิทธิภาพเฉพาะโดเมน Microsoft เสนอทางเลือกที่ยั่งยืนซึ่งช่วยลดต้นทุนการคำนวณและผลกระทบต่อสิ่งแวดล้อม
ที่เกี่ยวข้อง: การจัดตำแหน่งอย่างรอบคอบ: กลยุทธ์ความปลอดภัยของ OpenAI สำหรับโมเดลการคิด o1 และ o3
ความสำเร็จของกรอบการทำงานในการให้เหตุผลทางคณิตศาสตร์เปิดประตูสู่การใช้งานในวงกว้าง ตั้งแต่การศึกษา สู่การวิจัยทางวิทยาศาสตร์
นักวิจัยวางแผนที่จะเผยแพร่โค้ดและข้อมูลของ rStar-Math บน GitHub เพื่อปูทางสำหรับการทำงานร่วมกันและการพัฒนาต่อไป ความโปร่งใสนี้สะท้อนให้เห็นถึงแนวทางของ Microsoft ในการสร้างเครื่องมือ AI ประสิทธิภาพสูงให้เข้าถึงได้สำหรับผู้ชมในวงกว้าง รวมถึงสถาบันการศึกษาและองค์กรขนาดกลาง
ที่เกี่ยวข้อง: การวิเคราะห์กึ่ง: ไม่ AI Scaling ไม่ใช่ ไม่ชะลอตัวลง
ในขณะที่การแข่งขันระหว่าง Microsoft และ OpenAI รุนแรงขึ้น ความก้าวหน้าที่นำเสนอโดย rStar-Math เน้นย้ำถึงศักยภาพของโมเดลขนาดเล็กเพื่อท้าทายการครอบงำของระบบที่ใหญ่กว่า ด้วยการจัดลำดับความสำคัญของประสิทธิภาพและความแม่นยำ rStar-Math ได้สร้างมาตรฐานใหม่สำหรับสิ่งที่ระบบ AI ขนาดกะทัดรัดสามารถทำได้
