Sztuczna inteligencja zależy od jej zdolności do interpretowania danych, dostosowywania się do dynamicznych środowisk i podejmowania decyzji na podstawie niekompletnych informacji. W sercu tych procesów leży entropia – metryka określająca ilościowo niepewność i losowość.
Początkowo entropia niegdyś wykorzystywana w termodynamice, entropia odgrywa teraz podstawową rolę w sztucznej inteligencji, kierując systemy równoważące strukturę z elastycznością i zwiększające ich zdolność do radzenia sobie ze złożonymi zadaniami.
Claude Shannon na nowo zdefiniował entropię w 1948 r.,
Dziś entropia napędza innowacje w uczeniu maszynowym, tworzeniu danych syntetycznych i modelach generatywnych , uczenie się przez wzmacnianie i obliczenia kwantowe. W miarę jak sztuczna inteligencja staje się coraz bardziej integralna z nowoczesnymi technologiami, zrozumienie zastosowań entropii jest kluczem do stworzenia inteligentniejszych, bardziej adaptacyjnych systemów.
Początki entropii
Entropia została wprowadzona po raz pierwszy w XIX wieku, kiedy naukowcy starali się zrozumieć efektywność energetyczną w układach termodynamicznych. Pionierskie badania Sadi Carnot nad ciepłem silniki inspirowane Rudolf Clausius, aby formalnie zdefiniować entropię.
Clausius opisał ją jako część energii w układzie, której nie można przekształcić w pracę, co odzwierciedla tendencję wszechświata do większego nieporządku. Ta termodynamiczna koncepcja położyła podwaliny pod zrozumienie losowości i nieodwracalności w układach fizycznych.
Przełom Claude’a Shannona
Claude Shannon zrewolucjonizował entropię, stosując ją w systemach informatycznych. W swojej przełomowej pracy A Mathematical Theory of Communication Shannon opisał entropię jako miara niepewności zbioru danych. Napisał: „Podstawowym problemem komunikacji jest odtworzenie w jednym punkcie dokładnie lub w przybliżeniu komunikatu wybranego w innym punkcie.”
Entropia Shannona określiła ilościowo nieprzewidywalność informacji, umożliwiając inżynierom obliczenie wydajności transmisja i kompresja danych. Jego formuła ustanowiła entropię jako uniwersalną metrykę pomiaru niepewności, łącząc ją z rozkładami prawdopodobieństwa i tworząc podstawę nowoczesnych technologii opartych na danych.
Entropia w maszynie. Uczenie się
W uczeniu maszynowym entropia ocenia losowość lub nieczystość w zbiorach danych, kierując algorytmami do podejmowania decyzji minimalizujących niepewność.
Drzewa decyzyjne wykorzystują entropię do określenia podziałów dostarczających najwięcej informacji. Atrybuty, które maksymalizują przyrost informacji lub redukcję entropii, to wybrane jako kryteria podziału, poprawiające dokładność klasyfikacji modelu.
Rozważ zbiór danych z etykietami klas mieszanych: jego wysoka entropia odzwierciedla nieprzewidywalność. Dzieląc dane na podzbiory w oparciu o określony atrybut, entropia ulega zmniejszeniu, co skutkuje bardziej jednorodnymi grupami.
Ten iteracyjny proces buduje drzewo decyzyjne, które systematycznie obniża niepewność, tworząc strukturę zoptymalizowaną pod kątem dokładnych przewidywań.
Wzór na uzyskanie informacji jest następujący:
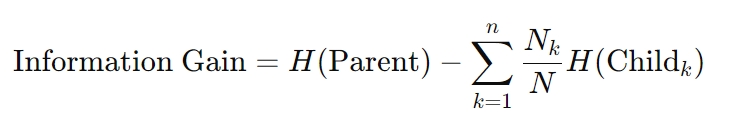
Tutaj H oznacza entropię, Nk oznacza liczbę próbek w k-tym węźle podrzędnym, a N strong> to całkowita liczba próbek w węźle nadrzędnym. Obliczenia te zapewniają, że każda decyzja maksymalnie zmniejsza niepewność, co jest zasadą leżącą u podstaw algorytmów drzew decyzyjnych.
Strata krzyżowa entropii w sieciach neuronowych
Entropia również leży u podstaw optymalizacji Techniki w sieciach neuronowych. Strata krzyżowa, metryka szeroko stosowana w zadaniach klasyfikacyjnych, mierzy rozbieżność między przewidywanymi prawdopodobieństwami i rzeczywiste etykiety. Minimalizowanie tej straty dopasowuje przewidywania modelu do wyników w świecie rzeczywistym, zwiększając dokładność.
Wzór na stratę krzyżową entropii to:
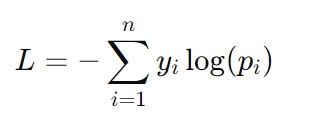
Tutaj, yi reprezentuje rzeczywistą etykietę (np. 0 lub 1), a pi to przewidywane prawdopodobieństwo tej etykiety. Utrata entropii krzyżowej jest szczególnie istotna w zadaniach takich jak rozpoznawanie obrazów i modelowanie języka, gdzie do osiągnięcia sukcesu konieczne jest dokładne przewidywanie prawdopodobieństwa.
Rola entropii w tworzeniu danych syntetycznych
Dane syntetyczne stały się kluczowym zasobem w rozwoju sztucznej inteligencji, oferującym rozwiązania problemów takich jak ograniczony dostęp do rzeczywistych zbiorów danych, obawy dotyczące prywatności i ograniczenia kosztowe.
Jednak skuteczność syntetycznych zbiorów danych zależy w dużym stopniu od ich poziomu entropii. Dane syntetyczne o wysokiej entropii wprowadzają zmienność potrzebną do naśladowania warunków w świecie rzeczywistym, umożliwiając modelom sztucznej inteligencji lepsze uogólnianie nowych scenariuszy.
Jednak nadmierna entropia może wprowadzić szum, co prowadzi do overfitting — gdy model zostaje nadmiernie dostrojony do uczenia danych i nie radzi sobie dobrze z niewidocznymi przykładami.
Z kolei zbiory danych o niskiej entropii upraszczają naukę, ale mogą nie odzwierciedlać złożoności danych ze świata rzeczywistego. Ta nierównowaga stwarza ryzyko niedopasowania, w przypadku którego modele nie potrafią uchwycić znaczących wzorców, co skutkuje słabą generalizacją. Znalezienie właściwej równowagi pomiędzy tymi skrajnościami jest kluczem do tworzenia wysokiej jakości danych syntetycznych.
Techniki optymalizacji danych syntetycznych za pomocą entropii
Aby sprostać stawianym wyzwaniom dzięki entropii w syntetycznych zbiorach danych badacze stosują zaawansowane techniki, które poprawiają jakość danych, zachowując jednocześnie ich przydatność:
Selekcja entropii z rzeczywistą syntetyczną maksymalizacją podobieństwa (ESRM): ESRM identyfikuje próbki syntetyczne, które ściśle odzwierciedlają dane ze świata rzeczywistego, zapewnienie, że zbiory danych szkoleniowych pozostaną zróżnicowane, a jednocześnie łatwe w zarządzaniu. Równoważenie entropii w syntetycznych zbiorach danych zapewnia uczenie modeli na różnorodnych, ale odpowiednich przykładach, redukując szumy przy jednoczesnym zachowaniu użyteczności. Czyszczenie i normalizacja danych: procesy te pomagają wyeliminować nadmierną losowość, dopasowując rozkłady danych syntetycznych do rozkładów danych w świecie rzeczywistym. Normalizacja zapewnia zgodność zbiorów danych z algorytmami uczenia maszynowego, ułatwiając płynniejszą zbieżność modeli. Wybór funkcji: koncentrując się na funkcjach bogatych w entropię, które zapewniają najwięcej informacji, wybór funkcji zmniejsza redundancję i szum, dzięki czemu dane syntetyczne są bardziej skuteczne w szkoleniu modeli.
Te metody zwiększają wiarygodność danych syntetycznych, pomagając systemom AI w osiąganiu solidnych uogólnień bez nadmiernego lub niedopasowania.
Generatywna sztuczna inteligencja: kreatywność i kontrola poprzez entropię
Generatywna sztuczna inteligencja, obejmująca systemy takie jak generatory tekstu, kreatory obrazów i narzędzia do syntezy dźwięku, wykorzystuje entropię do kontrolowania równowagi między kreatywnością a spójnością.
Dostosowując progi entropii, programiści mogą wpływać na przewidywalność i różnorodność generowanych wyników.
Na przykład ustawienie niskiej entropii zapewnia skupienie i trafność odpowiedzi, co idealnie sprawdza się w zastosowaniach takich jak chatboty obsługi klienta lub zautomatyzowani asystenci pisania. Z drugiej strony wyższa entropia wprowadza różnorodność i nowość, umożliwiając kreatywne zadania, takie jak tworzenie dzieł sztuki lub opowiadanie historii.
Ta kontrola ma kluczowe znaczenie dla dostosowania generatywnej sztucznej inteligencji do konkretnych przypadków użycia. W praktycznych zastosowaniach korekty entropii pomagają zachować równowagę między innowacyjnością a precyzją, zapewniając, że wyniki spełniają pożądane cele bez utraty jakości.
Uwierzytelnianie treści generowanych przez sztuczną inteligencję
Entropia odgrywa również istotną rolę w weryfikacji autentyczności treści generowanych przez sztuczną inteligencję. Badania wykazały, że tekst wygenerowany przez sztuczną inteligencję ma zwykle niższą entropię w porównaniu z materiałem napisanym przez człowieka, co ułatwia jego wykrycie.
Ta mierzalna luka stanowi punkt odniesienia umożliwiający odróżnienie treści syntetycznych od autentycznych wyrażeń ludzkich.
Takie wskaźniki mają praktyczne zastosowanie w zwalczaniu dezinformacji i zapewnianiu integralności treści generowanych przez sztuczną inteligencję. Organizacje korzystają z analizy entropii, aby zidentyfikować potencjalne niewłaściwe wykorzystanie generatywnej sztucznej inteligencji w deepfakes, fałszywych wiadomościach lub automatycznej propagandzie, podkreślając jej rosnące znaczenie w weryfikacji treści.
Uczenie się przez wzmacnianie: odkrywanie nieznanego za pomocą entropii
W uczenie się przez wzmacnianie (RL), entropia ma kluczowe znaczenie dla utrzymania delikatnej równowagi między eksploracją a eksploatacją. Eksploracja polega na próbowaniu nowych działań w celu odkrycia lepszych strategii, podczas gdy eksploatacja koncentruje się na udoskonalaniu znanych działań w celu maksymalizacji korzyści. Polityka wysokiej entropii zachęca do zróżnicowanego wyboru działań, zapobiegając utknięciu agentów w nieoptymalnych rozwiązaniach.
Zasada ta jest szczególnie cenna w dynamicznych środowiskach, takich jak autonomiczna robotyka, sztuczna inteligencja do gier i adaptacyjne systemy logistyczne, gdzie elastyczność i zdolność adaptacji są niezbędne.
Regularyzacja entropii — technika wprowadzająca karę na podstawie entropii polityki — gwarantuje, że agenci zachowają wystarczająca losowość, aby badać alternatywne strategie bez uszczerbku dla długoterminowej wydajności.
Stabilizacja uczenia się za pomocą Entropii
Metody gradientu polityki, klasa algorytmów RL, również korzystają ze stabilizującego efektu entropii. Utrzymując kontrolowaną losowość w procesie decyzyjnym agenta, entropia zapobiega przedwczesnej zbieżności i sprzyja bardziej wszechstronnej eksploracji.
Entropia zapewnia, że agenci uczenia się przez wzmacnianie zachowują zdolność adaptacji, co pozwala im rozwijać się w złożonych i nieprzewidywalnych środowiskach.
Entropia w obliczeniach kwantowych i kompresji danych
W obliczeniach kwantowych entropia odgrywa kluczową rolę w ocenie spójności i splątanie stanów kwantowych. W przeciwieństwie do systemów klasycznych, w których entropia określa ilościowo nieporządek w rozkładach danych, entropia kwantowa oddaje probabilistyczny charakter systemów kwantowych.
Metryki takie jak entropia Neumanna są powszechnie stosowane do pomiaru niepewności i pomagają w optymalizacji hybrydowych układów kwantowych algorytmy klasyczne.
Algorytmy te wykorzystują entropię kwantową do rozwiązywania problemów, które są niewykonalne obliczeniowo w przypadku klasycznych systemów, takich jak złożone zadania optymalizacyjne, kryptografia i symulacje struktur molekularnych.
Na przykład entropia von Neumanna odgrywa kluczową rolę w udoskonalaniu kwantowych sieci neuronowych, które łączą probabilistyczne zasady mechaniki kwantowej z tradycyjnymi strukturami uczenia maszynowego. Entropia zasadniczo łączy niepewność właściwą mechanice kwantowej z przewidywalnością wymaganą w systemach klasycznych.
Entropia kwantowa pomaga również w korekcji błędów, co jest kluczowym wyzwaniem w obliczeniach kwantowych. Identyfikując i minimalizując źródła entropii w układach kwantowych, programiści mogą poprawić stabilność i niezawodność kubitów, torując drogę dla bardziej niezawodnych technologii kwantowych.
Kompresja danych oparta na entropii
Entropia stanowi podstawę algorytmów kompresji danych, umożliwiając wydajne przechowywanie i przesyłanie przez ograniczenie redundancji przy jednoczesnym zachowaniu istotnych informacji. Techniki kompresji analizują poziomy entropii w zbiorach danych w celu optymalizacji schematów kodowania, zachowując równowagę pomiędzy minimalizacją rozmiarów plików i zachowaniem integralności danych.
To podejście jest szczególnie przydatne w środowiskach o ograniczonej przepustowości, takich jak sieci IoT i systemy przetwarzania brzegowego.
Na przykład metody kompresji opartej na entropii umożliwiają urządzeniom IoT skuteczniejsze przesyłanie danych z czujników, zmniejszając zużycie energii i wykorzystanie przepustowości. Wykorzystując entropię jako wiodącą metrykę, systemy te osiągają wysoką wydajność bez uszczerbku dla dokładności i niezawodności.
Względy etyczne: włączenie, stronniczość i przejrzystość
Zbiory danych o wysokiej entropii często zawierają różnorodne i mniej powszechne przykłady, takie jak dane reprezentujące niedostatecznie reprezentowane grupy. Te punkty danych są niezbędne do budowania sprawiedliwych systemów sztucznej inteligencji, ale można je przypadkowo wykluczyć podczas procesów optymalizacji entropii, co prowadzi do stronniczych wyników.
Programiści muszą zadbać o to, aby techniki oparte na entropii uwzględniały wszystkie istotne punkty danych, aby zapobiec wykluczeniu grup marginalizowanych.
W sztucznej inteligencji entropia określa ilościowo niepewność, naszym obowiązkiem jest zapewnienie że sposób, w jaki sobie z tym radzimy, odzwierciedla zaangażowanie na rzecz uczciwości i inkluzywności. Tworzenie przejrzystych systemów, w których priorytetem jest włączenie, nie tylko poprawia sprawiedliwość, ale także zwiększa solidność modeli sztucznej inteligencji, wystawiając je na szerszy zakres scenariuszy.
Przejrzystość w podejmowaniu decyzji w oparciu o entropię
Ponieważ systemy sztucznej inteligencji w coraz większym stopniu opierają się na entropii przy podejmowaniu decyzji, utrzymanie przejrzystości staje się krytyczne. Jest to szczególnie prawdziwe w przypadku wrażliwych zastosowań, takich jak opieka zdrowotna i podejmowanie decyzji prawnych, gdzie stawka jest wysoka.
Wyjaśnienie, w jaki sposób metryki entropii wpływają na przewidywania modeli lub decyzje, jest niezbędne do budowania zaufania i zapewnienia odpowiedzialności.
Na przykład w medycznej sztucznej inteligencji entropia jest często używana do pomiaru niepewności prognoz diagnostycznych. Komunikując tę niepewność pracownikom służby zdrowia, systemy te umożliwiają podejmowanie bardziej świadomych decyzji, wypełniając lukę między wynikami algorytmów a ludzką wiedzą.
Rozszerzanie roli entropii w sztucznej inteligencji
Kwantowa sztuczna inteligencja reprezentuje konwergencję sztucznej inteligencji i obliczeń kwantowych, a entropia jest sercem tego skrzyżowania. Naukowcy badają, w jaki sposób wskaźniki entropii kwantowej, takie jak entropia von Neumanna, mogą optymalizować kwantowe sieci neuronowe i inne systemy hybrydowe.
Te postępy są obiecujące w rozwiązywaniu złożonych problemów w takich dziedzinach, jak logistyka, odkrywanie leków i bezpieczna komunikacja.
Na przykład systemy kwantowej sztucznej inteligencji mogłyby wykorzystać entropię do modelowania skomplikowanych interakcji molekularnych z niespotykanymi dotychczas precyzję, przyspieszając przełomy w farmacji. Łącząc probabilistyczne zalety systemów kwantowych z możliwościami adaptacji sztucznej inteligencji, entropia w dalszym ciągu zwiększa swój wpływ w najnowocześniejszych technologiach.
Integracja między przepływami pracy AI
Entropy jest coraz częściej integrowana na każdym etapie przepływów pracy AI, od wstępnego przetwarzania danych po podejmowanie decyzji w czasie rzeczywistym. Służy jako ujednolicająca miara do ilościowego określania niepewności, umożliwiając systemom dynamiczne dostosowywanie się do zmieniających się warunków.
Ta integracja gwarantuje, że sztuczna inteligencja pozostanie elastyczna, niezawodna i zdolna do stawienia czoła wyzwaniom złożonych środowisk.
Branże, od pojazdów autonomicznych po modelowanie finansowe, korzystają z podejść opartych na entropii, które zwiększyć dokładność przewidywań, szybkość podejmowania decyzji i zdolność adaptacji. Osadzając entropię w rdzeniu rozwoju sztucznej inteligencji, badacze budują systemy, które są nie tylko solidne technicznie, ale także zgodne z celami etycznymi i społecznymi.
Co nas czeka
Entropia ewoluowała od koncepcji termodynamicznej do kamienia węgielnego sztucznej inteligencji. Kwantownie określając niepewność, umożliwia systemom sztucznej inteligencji zrównoważenie losowości i struktury, wspierając zdolności adaptacyjne, kreatywność i precyzję. Niezależnie od tego, czy kierujemy algorytmami uczenia maszynowego, zarządzamy danymi syntetycznymi, czy wprowadzamy innowacje w zakresie sztucznej inteligencji kwantowej, wyraźnie widzimy, jak entropia zmienia sposób, w jaki sztuczna inteligencja uczy się i dostosowuje.
Wraz ze wzrostem złożoności i wpływu sztucznej inteligencji, zrozumienie i zastosowanie entropii będzie niezbędne do budowania systemów, które będą nie tylko mądrzejsze, ale także sprawiedliwsze, bardziej przejrzyste i lepiej przygotowane do radzenia sobie z niepewnością prawdziwego świata.
