L’intelligenza artificiale dipende dalla sua capacità di interpretare i dati, adattarsi ad ambienti dinamici e prendere decisioni con informazioni incomplete. Al centro di questi processi c’è l’entropia, una metrica che quantifica l’incertezza e la casualità.
Originariamente cconcepita nella termodinamica, l’entropia ora gioca un ruolo fondamentale nell’intelligenza artificiale, guidando sistemi per bilanciare la struttura con la flessibilità e migliorare la loro capacità di gestire compiti complessi.
Claude Shannon ha ridefinito l’entropia nel 1948, trasformandola in una misura di incertezza per i sistemi informativi. Il lavoro di Shannon ha fornito un quadro matematico per ottimizzare la trasmissione dei dati e le sue intuizioni sono ora integrate nelle discipline dell’intelligenza artificiale.
Oggi, l’entropia guida le innovazioni nell’apprendimento automatico, nella creazione di dati sintetici e nei modelli generativi , apprendimento per rinforzo e calcolo quantistico. Man mano che l’intelligenza artificiale diventa sempre più parte integrante delle tecnologie moderne, comprendere le applicazioni dell’entropia è fondamentale per sistemi più intelligenti e adattivi.
Le origini dell’entropia
L’entropia è stata introdotta per la prima volta nel 19° secolo, quando gli scienziati cercarono di comprendere l’efficienza energetica nei sistemi termodinamici. Studi pionieristici Sadi Carnot sul calore motori hanno ispirato Rudolf Clausius a definire formalmente l’entropia.
Clausius lo descrisse come la porzione di energia di un sistema che non può essere convertita in lavoro, riflettendo la tendenza dell’universo verso un maggiore disordine. Questo concetto termodinamico ha gettato le basi per comprendere la casualità e l’irreversibilità nei sistemi fisici.
La svolta di Claude Shannon
Claude Shannon ha rivoluzionato l’entropia applicandola ai sistemi di informazione. Nel suo articolo fondamentale A Mathematical Theory of Communication, Shannon ha descritto l’entropia come una misura dell’incertezza in un set di dati. Scrisse:”Il problema fondamentale della comunicazione è quello di riprodurre in un punto, esattamente o approssimativamente, un messaggio selezionato in un altro punto.”
L’entropia di Shannon quantifica l’imprevedibilità delle informazioni, consentendo agli ingegneri di calcolare l’efficienza di trasmissione e compressione dei dati. La sua formula stabilì l’entropia come metrica universale per misurare l’incertezza, collegandola alle distribuzioni di probabilità e creando una base per le moderne tecnologie basate sui dati.
Entropia nella macchina. Apprendimento
Nell’apprendimento automatico, l’entropia valuta la casualità o l’impurità all’interno dei set di dati, guidando gli algoritmi a prendere decisioni che riducono al minimo l’incertezza. en.wikipedia.org/wiki/Decision_tree”>Alberi decisionali, ad esempio, utilizzano l’entropia per determinare le suddivisioni più informative. Gli attributi che massimizzano il guadagno di informazioni, o la riduzione dell’entropia, vengono scelti come criteri di suddivisione, migliorando la classificazione del modello precisione.
Considera un set di dati con etichette di classi miste: la sua elevata entropia riflette l’imprevedibilità. Dividendo i dati in sottoinsiemi basati su un attributo specifico, l’entropia viene ridotta, risultando in gruppi più omogenei.
Questo processo iterativo crea un albero decisionale che riduce sistematicamente l’incertezza, creando una struttura ottimizzata per previsioni accurate.
La formula per l’acquisizione di informazioni è la seguente:
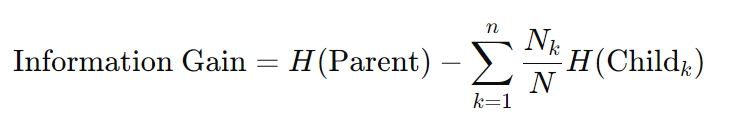
Qui, H rappresenta l’entropia, Nk è il conteggio dei campioni nel nodo figlio k-esimo e N è il totale conteggio dei campioni nel nodo padre. Questo calcolo garantisce che ogni decisione riduca al massimo l’incertezza, un principio fondamentale per gli algoritmi dell’albero decisionale.
Perdita incrociata di entropia nelle reti neurali
L’entropia è anche alla base dell’ottimizzazione tecniche nelle reti neurali. La Perdita di entropia incrociata, una metrica ampiamente utilizzata nei compiti di classificazione, misura la divergenza tra le probabilità previste e etichette vere e proprie. Riducendo al minimo questa perdita si allineano le previsioni di un modello con i risultati del mondo reale, migliorando la precisione.
La formula per la perdita di entropia incrociata è:
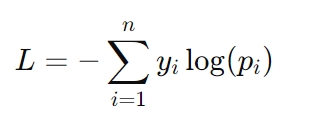
Ecco, yi rappresenta l’etichetta effettiva (ad esempio, 0 o 1) e pi è la probabilità prevista per quell’etichetta. La perdita di entropia incrociata è particolarmente critica in attività come il riconoscimento delle immagini e la modellazione del linguaggio, dove per avere successo sono necessarie previsioni precise di probabilità.
Il ruolo dell’entropia nella creazione di dati sintetici
I dati sintetici sono diventati una risorsa fondamentale nello sviluppo dell’intelligenza artificiale, offrendo soluzioni a sfide come l’accesso limitato a set di dati del mondo reale, problemi di privacy e vincoli di costo.
Tuttavia, l’efficacia dei set di dati sintetici dipende fortemente dai loro livelli di entropia. I dati sintetici ad alta entropia introducono la variabilità necessaria per imitare le condizioni del mondo reale, consentendo ai modelli di intelligenza artificiale di generalizzarsi meglio a nuovi scenari.
Tuttavia, un’entropia eccessiva può introdurre rumore, portando a overfitting—dove il modello diventa eccessivamente sintonizzato sui dati di addestramento e non riesce a funzionare bene su esempi mai visti.
Al contrario, i set di dati a bassa entropia semplificano l’apprendimento ma possono sottorappresentare la complessità dei dati del mondo reale. Questo squilibrio rischia di underfitting, in cui i modelli non riescono a catturare modelli significativi, con conseguente scarsa generalizzazione. Trovare il giusto equilibrio tra questi estremi è fondamentale per creare dati sintetici di alta qualità.
Tecniche per l’ottimizzazione dei dati sintetici con l’entropia
Per affrontare le sfide poste dall’entropia nei set di dati sintetici, i ricercatori utilizzano tecniche avanzate che migliorano la qualità dei dati mantenendone la pertinenza:
Selezione dell’entropia con massimizzazione della somiglianza reale-sintetica (ESRM): ESRM identifica campioni sintetici che rispecchiano fedelmente i dati del mondo reale, garantire che i set di dati di addestramento rimangano diversificati ma gestibili. Il bilanciamento dell’entropia nei set di dati sintetici garantisce che i modelli siano addestrati su esempi diversi ma rilevanti, riducendo il rumore e preservando l’utilità. Pulizia e normalizzazione dei dati: questi processi aiutano a eliminare l’eccessiva casualità allineando le distribuzioni dei dati sintetici con quelle dei set di dati del mondo reale. La normalizzazione garantisce che i set di dati siano compatibili con gli algoritmi di machine learning, facilitando una convergenza più fluida dei modelli. Selezione delle funzionalità: concentrandosi sulle funzionalità ricche di entropia che forniscono gli approfondimenti più informativi, la selezione delle funzionalità riduce la ridondanza e il rumore, rendendo i dati sintetici più efficaci per l’addestramento del modello.
Questi metodi migliorano l’affidabilità dei dati sintetici, aiutando i sistemi di intelligenza artificiale a raggiungere una solida generalizzazione senza adattamento eccessivo o insufficiente.
AI generativa: creatività e controllo attraverso l’entropia
L’intelligenza artificiale generativa, che include sistemi come generatori di testo, creatori di immagini e strumenti di sintesi audio, si basa sull’entropia per controllare l’equilibrio tra creatività e coerenza.
Regolando le soglie di entropia, gli sviluppatori possono influenzare quanto prevedibili o vari siano gli output generati.
Ad esempio, un’impostazione a bassa entropia garantisce che le risposte siano mirate e pertinenti, ideali per applicazioni come chatbot del servizio clienti o assistenti di scrittura automatizzati. Al contrario, un’entropia più elevata introduce diversità e novità, consentendo attività creative come la generazione di opere d’arte o la narrazione.
Questo controllo è fondamentale per adattare l’IA generativa a casi d’uso specifici. Nelle applicazioni pratiche, gli aggiustamenti dell’entropia aiutano a mantenere un equilibrio tra innovazione e precisione, garantendo che i risultati raggiungano gli obiettivi desiderati senza compromettere la qualità.
Autenticazione dei contenuti generati dall’intelligenza artificiale
L’entropia svolge anche un ruolo fondamentale nel verificare l’autenticità dei contenuti generati dall’intelligenza artificiale. Gli studi hanno dimostrato che il testo generato dall’intelligenza artificiale tende a mostrare un’entropia inferiore rispetto al materiale scritto dall’uomo, rendendolo più facile da rilevare.
Questo divario misurabile fornisce un punto di riferimento per distinguere i contenuti sintetici dalle espressioni umane autentiche.
Tali metriche hanno applicazioni pratiche nella lotta alla disinformazione e nel garantire l’integrità dei contenuti generati dall’intelligenza artificiale. Le organizzazioni utilizzano l’analisi entropica per identificare il potenziale uso improprio dell’intelligenza artificiale generativa nei deepfake, nelle notizie false o nella propaganda automatizzata, evidenziandone l’importanza crescente nella verifica dei contenuti.
Apprendimento per rinforzo: esplorare l’ignoto con l’entropia
In apprendimento per rinforzo (RL), L’entropia è fondamentale per mantenere il delicato equilibrio tra esplorazione e sfruttamento. L’esplorazione implica provare nuove azioni per scoprire strategie migliori, mentre lo sfruttamento si concentra sul perfezionamento di azioni conosciute per massimizzare i guadagni. Le politiche ad alta entropia incoraggiano una selezione diversificata delle azioni, impedendo agli agenti di rimanere bloccati in soluzioni non ottimali.
Questo principio è particolarmente prezioso in ambienti dinamici, come la robotica autonoma, l’intelligenza artificiale dei videogiochi e i sistemi logistici adattivi, dove flessibilità e adattabilità sono essenziali.
regolarizzazione dell’entropia, una tecnica che introduce un termine di penalità basato sull’entropia della policy, garantisce che gli agenti mantengano casualità sufficiente per esplorare strategie alternative senza compromettere le prestazioni a lungo termine.
Stabilizzare l’apprendimento con l’entropia
L’entropia garantisce che gli agenti dell’apprendimento per rinforzo rimangano adattabili, consentendo loro di prosperare in ambienti complessi e imprevedibili.
Entropia nell’informatica quantistica e nella compressione dei dati
Nell’informatica quantistica, l’entropia gioca un ruolo fondamentale nella valutazione della coerenza e dell’entanglement dei sistemi quantistici stati. A differenza dei sistemi classici, dove l’entropia quantifica il disordine nella distribuzione dei dati, l’entropia quantistica cattura la natura probabilistica dei sistemi quantistici.
Metriche come von entropia di Neumann sono ampiamente utilizzate per misurare l’incertezza e guidare l’ottimizzazione dell’entropia quantistica ibrida algoritmi classici.
Questi algoritmi sfruttano l’entropia quantistica per risolvere problemi che sono computazionalmente irrealizzabili per i sistemi classici, come compiti complessi di ottimizzazione, crittografia e simulazioni di strutture molecolari.
Ad esempio, l’entropia di von Neumann è determinante nel perfezionare le reti neurali quantistiche, che fondono i principi probabilistici della meccanica quantistica con i tradizionali quadri di apprendimento automatico. L’entropia fondamentalmente collega l’incertezza insita nella meccanica quantistica con la prevedibilità richiesta dai sistemi classici.
L’entropia quantistica aiuta anche nella correzione degli errori, una sfida chiave nell’informatica quantistica. Identificando e riducendo al minimo le fonti di entropia all’interno dei sistemi quantistici, gli sviluppatori possono migliorare la stabilità e l’affidabilità dei qubit, aprendo la strada a tecnologie quantistiche più robuste.
Compressione dei dati basata sull’entropia
L’entropia è alla base degli algoritmi di compressione dei dati, consentendo un’archiviazione e una trasmissione efficienti riducendo la ridondanza e preservando elementi essenziali informazioni. Le tecniche di compressione analizzano i livelli di entropia all’interno dei set di dati per ottimizzare gli schemi di codifica, trovando un equilibrio tra la riduzione al minimo delle dimensioni dei file e il mantenimento dell’integrità dei dati.
Questo approccio è particolarmente utile in ambienti con limiti di larghezza di banda come le reti IoT e i sistemi di edge computing.
Ad esempio, i metodi di compressione basati sull’entropia consentono ai dispositivi IoT di trasmettere i dati dei sensori in modo più efficiente, riducendo il consumo energetico e l’utilizzo della larghezza di banda. Sfruttando l’entropia come metrica guida, questi sistemi raggiungono prestazioni elevate senza compromettere l’accuratezza o l’affidabilità.
Considerazioni etiche: inclusività, pregiudizi e trasparenza
I set di dati ad alta entropia spesso includono esempi diversi e meno comuni, come i dati che rappresentano gruppi sottorappresentati. Questi dati sono essenziali per costruire sistemi di intelligenza artificiale equi, ma possono essere inavvertitamente esclusi durante i processi di ottimizzazione dell’entropia, portando a risultati distorti.
Gli sviluppatori devono garantire che le tecniche basate sull’entropia tengano conto di tutti i dati rilevanti per prevenire l’esclusione di gruppi emarginati.
Nell’intelligenza artificiale, mentre l’entropia quantifica l’incertezza, è nostra responsabilità garantire che il modo in cui gestiamo la situazione riflette un impegno per l’equità e l’inclusività. Costruire sistemi trasparenti che diano priorità all’inclusività non solo migliora l’equità, ma aumenta anche la robustezza dei modelli di intelligenza artificiale esponendoli a una gamma più ampia di scenari.
Trasparenza nel processo decisionale basato sull’entropia
Poiché i sistemi di intelligenza artificiale fanno sempre più affidamento sull’entropia per guidare il processo decisionale, mantenere la trasparenza diventa fondamentale. Ciò è particolarmente vero in applicazioni sensibili come l’assistenza sanitaria e il processo decisionale legale, dove la posta in gioco è alta.
Spiegare in che modo le metriche entropiche influenzano le previsioni o le decisioni dei modelli è fondamentale per creare fiducia e garantire la responsabilità.
Ad esempio, nell’intelligenza artificiale medica, l’entropia viene spesso utilizzata per misurare l’incertezza nelle previsioni diagnostiche. Comunicando questa incertezza agli operatori sanitari, questi sistemi consentono un processo decisionale più informato, colmando il divario tra i risultati algoritmici e le competenze umane.
Espandere il ruolo dell’entropia nell’intelligenza artificiale
L’intelligenza artificiale quantistica rappresenta una convergenza tra intelligenza artificiale e calcolo quantistico e l’entropia è al centro di questa intersezione. I ricercatori stanno studiando come le metriche dell’entropia quantistica, come l’entropia di von Neumann, possano ottimizzare le reti neurali quantistiche e altri sistemi ibridi.
Questi progressi sono promettenti per la risoluzione di problemi complessi in campi come la logistica, la scoperta di farmaci e le comunicazioni sicure.
Ad esempio, i sistemi di intelligenza artificiale quantistica potrebbero sfruttare l’entropia per modellare complesse interazioni molecolari con risultati senza precedenti. precisione, accelerando le scoperte nel settore farmaceutico. Combinando i punti di forza probabilistici dei sistemi quantistici con l’adattabilità dell’intelligenza artificiale, l’entropia continua ad espandere la sua influenza nelle tecnologie all’avanguardia.
Integrazione nei flussi di lavoro dell’intelligenza artificiale
L’entropia viene sempre più integrata in ogni fase dei flussi di lavoro dell’intelligenza artificiale, dalla preelaborazione dei dati al processo decisionale in tempo reale. Serve come metrica unificante per quantificare l’incertezza, consentendo ai sistemi di adattarsi dinamicamente alle mutevoli condizioni.
Questa integrazione garantisce che l’intelligenza artificiale rimanga flessibile, affidabile e in grado di affrontare le sfide di ambienti complessi.
I settori che vanno dai veicoli autonomi alla modellazione finanziaria beneficiano di approcci basati sull’entropia, che migliorare l’accuratezza delle previsioni, la velocità del processo decisionale e l’adattabilità. Incorporando l’entropia al centro dello sviluppo dell’intelligenza artificiale, i ricercatori stanno costruendo sistemi che non sono solo tecnicamente robusti ma anche allineati con obiettivi etici e sociali.
Ciò che ci aspetta
L’entropia si è evoluta da un concetto termodinamico a una pietra angolare dell’intelligenza artificiale. Quantificando l’incertezza, consente ai sistemi di intelligenza artificiale di bilanciare casualità e struttura, favorendo adattabilità, creatività e precisione. Che si tratti di guidare algoritmi di apprendimento automatico, gestire dati sintetici o guidare innovazioni di intelligenza artificiale quantistica, possiamo vedere chiaramente come l’entropia stia rimodellando il modo in cui l’intelligenza artificiale apprende e si adatta.
Mentre l’intelligenza artificiale continua a crescere in complessità e impatto, la comprensione e applicare l’entropia sarà essenziale per costruire sistemi che siano non solo più intelligenti ma anche più giusti, più trasparenti e meglio attrezzati per affrontare le incertezze del mondo reale.