La inteligencia artificial depende de su capacidad para interpretar datos, adaptarse a entornos dinámicos y tomar decisiones con información incompleta. En el centro de estos procesos se encuentra la entropía, una métrica que cuantifica la incertidumbre y la aleatoriedad.
Originalmente cconcebida en termodinámica, la entropía ahora juega un papel fundamental en la IA, guiando sistemas para equilibrar la estructura con la flexibilidad y mejorar su capacidad para manejar tareas complejas.
Claude Shannon redefinió la entropía en 1948, transformándola en una medida de incertidumbre para los sistemas de información. El trabajo de Shannon proporcionó un marco matemático para optimizar la transmisión de datos, y sus conocimientos ahora están integrados en todas las disciplinas de la IA.
Hoy en día, la entropía impulsa las innovaciones en el aprendizaje automático, la creación de datos sintéticos y los modelos generativos. , aprendizaje por refuerzo y computación cuántica. A medida que la IA se vuelve más integral para las tecnologías modernas, comprender las aplicaciones de la entropía es clave para lograr sistemas más inteligentes y adaptables.
Los orígenes de la entropía
La entropía se introdujo por primera vez en el siglo XIX cuando los científicos buscaban comprender la eficiencia energética en los sistemas termodinámicos. Los estudios pioneros de Sadi Carnot sobre el calor motores inspiraron a Rudolf Clausius para definir entropía formalmente.
Clausio lo describió como la porción de energía de un sistema que no se puede convertir en trabajo, lo que refleja la tendencia del universo hacia un mayor desorden. Este concepto termodinámico sentó las bases para comprender la aleatoriedad y la irreversibilidad en los sistemas físicos.
El avance de Claude Shannon
Claude Shannon revolucionó la entropía aplicándola a los sistemas de información. En su artículo fundamental Una teoría matemática de la comunicación, Shannon describió la entropía como una medida de incertidumbre en un conjunto de datos. Escribió:”El problema fundamental de la comunicación es el de reproducir en un punto exactamente o aproximadamente un mensaje seleccionado en otro punto”.
La entropía de Shannon cuantificó la imprevisibilidad de la información, lo que permitió a los ingenieros calcular la eficiencia de transmisión y compresión de datos. Su fórmula estableció la entropía como una métrica universal para medir la incertidumbre, vinculándola a las distribuciones de probabilidad y creando una base para las tecnologías modernas basadas en datos.
Entropía en la máquina. Aprendizaje
En el aprendizaje automático, la entropía evalúa la aleatoriedad o la impureza dentro de los conjuntos de datos, guiando a los algoritmos para tomar decisiones que minimicen la incertidumbre
árboles de decisión, por ejemplo, utilizan la entropía para determinar las divisiones más informativas. Los atributos que maximizan la ganancia de información, o la reducción de la entropía, se eligen como criterios de división. mejorando la precisión de la clasificación del modelo.
Considere un conjunto de datos con etiquetas de clases mixtas: su alta entropía refleja imprevisibilidad. Al dividir los datos en subconjuntos en función de un atributo específico, se reduce la entropía, lo que da como resultado grupos más homogéneos.
Este proceso iterativo construye un árbol de decisiones que reduce sistemáticamente la incertidumbre, creando una estructura optimizada para predicciones precisas.
La fórmula para obtener información es la siguiente:
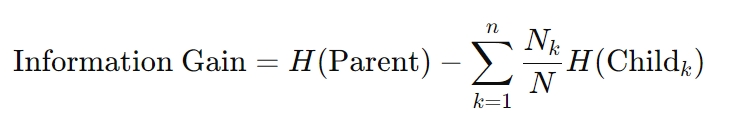
Aquí, H representa entropía, Nk es el recuento de muestras en el nodo secundario k-th y N es el total recuento de muestras en el nodo principal. Este cálculo garantiza que cada decisión reduzca al máximo la incertidumbre, un principio fundamental para los algoritmos de árboles de decisión.
Pérdida de entropía cruzada en redes neuronales
La entropía también sustenta la optimización Técnicas en redes neuronales. La pérdida de entropía cruzada, una métrica ampliamente utilizada en tareas de clasificación, mide la divergencia entre las probabilidades predichas y etiquetas reales. Minimizar esta pérdida alinea las predicciones de un modelo con los resultados del mundo real, mejorando la precisión.
La fórmula para la pérdida de entropía cruzada es:
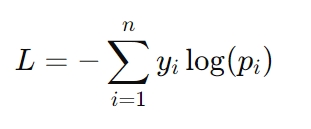
Aquí, yi representa la etiqueta real (por ejemplo, 0 o 1) y pi es la probabilidad prevista para esa etiqueta. La pérdida de entropía cruzada es especialmente crítica en tareas como el reconocimiento de imágenes y el modelado de lenguaje, donde se necesitan predicciones de probabilidad precisas para tener éxito.
El papel de la entropía en la creación de datos sintéticos
Los datos sintéticos se han convertido en un recurso crítico en el desarrollo de la IA, ya que ofrecen soluciones a desafíos como el acceso limitado a conjuntos de datos del mundo real, preocupaciones de privacidad y restricciones de costos.
Sin embargo, la eficacia de los conjuntos de datos sintéticos depende en gran medida de sus niveles de entropía. Los datos sintéticos de alta entropía introducen la variabilidad necesaria para imitar las condiciones del mundo real, lo que permite que los modelos de IA se generalicen mejor a nuevos escenarios.
Sin embargo, una entropía excesiva puede introducir ruido, lo que lleva a overfitting: donde el modelo se adapta demasiado a los datos de entrenamiento y no funciona bien en ejemplos invisibles.
Por el contrario, los conjuntos de datos de baja entropía simplifican el aprendizaje, pero pueden subestimar la complejidad de los datos del mundo real. Este desequilibrio corre el riesgo de un ajuste insuficiente, donde los modelos no logran capturar patrones significativos, lo que resulta en una generalización deficiente. Lograr el equilibrio adecuado entre estos extremos es clave para crear datos sintéticos de alta calidad.
Técnicas para optimizar datos sintéticos con entropía
Para abordar los desafíos planteados Por entropía en conjuntos de datos sintéticos, los investigadores emplean técnicas avanzadas que mejoran la calidad de los datos manteniendo la relevancia:
Selección de entropía con maximización de similitud real-sintética (ESRM): ESRM identifica muestras sintéticas que reflejan fielmente los datos del mundo real. garantizar que los conjuntos de datos de entrenamiento sigan siendo diversos pero manejables. Equilibrar la entropía en conjuntos de datos sintéticos garantiza que los modelos se entrenen en ejemplos diversos pero relevantes, lo que reduce el ruido y preserva la utilidad. Limpieza y normalización de datos: estos procesos ayudan a eliminar la aleatoriedad excesiva al alinear las distribuciones de datos sintéticos con las de conjuntos de datos del mundo real. La normalización garantiza que los conjuntos de datos sean compatibles con los algoritmos de aprendizaje automático, lo que facilita una convergencia de modelos más fluida. Selección de funciones: al centrarse en funciones ricas en entropía que proporcionan la información más informativa, la selección de funciones reduce la redundancia y el ruido, lo que hace que los datos sintéticos sean más eficaces para el entrenamiento de modelos.
Estos métodos mejoran la confiabilidad de los datos sintéticos, ayudando a los sistemas de IA a lograr una generalización sólida sin sobreajustes ni desajustes.
IA generativa: creatividad y control a través de la entropía
La IA generativa, que incluye sistemas como generadores de texto, creadores de imágenes y herramientas de síntesis de audio, se basa en la entropía para controlar el equilibrio entre creatividad y coherencia.
Al ajustar los umbrales de entropía, los desarrolladores pueden influir en cuán predecibles o variados son los resultados generados.
Por ejemplo, una configuración de baja entropía garantiza que las respuestas sean enfocadas y relevantes, ideal para aplicaciones como chatbots de servicio al cliente o asistentes de escritura automatizados. Por el contrario, una entropía más alta introduce diversidad y novedad, lo que permite tareas creativas como la generación de arte o la narración de historias.
Este control es fundamental para adaptar la IA generativa a casos de uso específicos. En aplicaciones prácticas, los ajustes de entropía ayudan a mantener un equilibrio entre innovación y precisión, asegurando que los resultados cumplan con los objetivos deseados sin comprometer la calidad.
Autenticar contenido generado por IA
Entropy también juega un papel vital en la verificación de la autenticidad del contenido generado por IA. Los estudios han demostrado que el texto generado por IA tiende a exhibir una entropía más baja en comparación con el material escrito por humanos, lo que lo hace más fácil de detectar.
Esta brecha mensurable proporciona un punto de referencia para distinguir el contenido sintético de las expresiones humanas auténticas.
Estas métricas tienen aplicaciones prácticas para combatir la desinformación y garantizar la integridad del contenido generado por IA. Las organizaciones utilizan el análisis de entropía para identificar el posible uso indebido de la IA generativa en deepfakes, noticias falsas o propaganda automatizada, destacando su creciente importancia en la verificación de contenido.
Aprendizaje por refuerzo: exploración de lo desconocido con entropía
En aprendizaje por refuerzo (RL), la entropía es fundamental para mantener el delicado equilibrio entre exploración y explotación. La exploración implica probar nuevas acciones para descubrir mejores estrategias, mientras que la explotación se centra en refinar acciones conocidas para maximizar las recompensas. Las políticas de alta entropía fomentan la selección de acciones diversas, evitando que los agentes se queden atrapados en soluciones subóptimas.
Este principio es especialmente valioso en entornos dinámicos, como la robótica autónoma, la inteligencia artificial para juegos y los sistemas de logística adaptativa, donde La flexibilidad y la adaptabilidad son esenciales.
regularización de entropía (una técnica que introduce un término de penalización basado en la entropía de la política) garantiza que los agentes retengan suficiente aleatoriedad para explorar estrategias alternativas sin comprometer el rendimiento a largo plazo.
Estabilización del aprendizaje con entropía
Métodos de gradiente de políticas, una clase de algoritmos RL, también se benefician de los efectos estabilizadores de la entropía. Al mantener una aleatoriedad controlada en el proceso de toma de decisiones del agente, la entropía previene la convergencia prematura y fomenta una exploración más integral.
La entropía garantiza que los agentes de aprendizaje por refuerzo sigan siendo adaptables, lo que les permite prosperar en entornos complejos e impredecibles.
Entropía en la computación cuántica y la compresión de datos
En la computación cuántica, la la entropía juega un papel crítico en la evaluación de la coherencia y el entrelazamiento de los procesos cuánticos. estados. A diferencia de los sistemas clásicos, donde la entropía cuantifica el desorden en las distribuciones de datos, la entropía cuántica captura la naturaleza probabilística de los sistemas cuánticos.
Métricas como la entropía de Neumann se utilizan ampliamente para medir la incertidumbre y guiar la optimización de las tecnologías cuánticas híbridas. algoritmos clásicos.
Estos algoritmos aprovechan la entropía cuántica para resolver problemas que son computacionalmente inviables para sistemas clásicos, como tareas complejas de optimización, criptografía y simulaciones de estructuras moleculares.
Por ejemplo, la entropía de von Neumann es fundamental para perfeccionar las redes neuronales cuánticas, que combinan los principios probabilísticos de la mecánica cuántica con los marcos tradicionales de aprendizaje automático. Básicamente, la entropía une la incertidumbre inherente a la mecánica cuántica con la previsibilidad que exigen los sistemas clásicos.
La entropía cuántica también ayuda en la corrección de errores, un desafío clave en la computación cuántica. Al identificar y minimizar las fuentes de entropía dentro de los sistemas cuánticos, los desarrolladores pueden mejorar la estabilidad y confiabilidad de los qubits, allanando el camino para tecnologías cuánticas más sólidas.
Compresión de datos basada en entropía
La entropía sustenta los algoritmos de compresión de datos, lo que permite un almacenamiento y transmisión eficientes al reducir la redundancia. preservando al mismo tiempo la información esencial. Las técnicas de compresión analizan los niveles de entropía dentro de los conjuntos de datos para optimizar los esquemas de codificación, logrando un equilibrio entre minimizar el tamaño de los archivos y conservar la integridad de los datos.
Este enfoque es particularmente valioso en entornos con ancho de banda limitado, como redes de IoT y sistemas informáticos de vanguardia.
Por ejemplo, los métodos de compresión basados en entropía permiten que los dispositivos de IoT transmitan datos de sensores de manera más eficiente. reduciendo el consumo de energía y el uso de ancho de banda. Al aprovechar la entropía como métrica guía, estos sistemas logran un alto rendimiento sin comprometer la precisión o la confiabilidad.
Consideraciones éticas: inclusión, parcialidad y transparencia
Los conjuntos de datos de alta entropía a menudo incluyen ejemplos diversos y menos comunes, como datos que representan grupos subrepresentados. Estos puntos de datos son esenciales para construir sistemas de IA equitativos, pero pueden excluirse inadvertidamente durante los procesos de optimización de la entropía, lo que genera resultados sesgados.
Los desarrolladores deben garantizar que las técnicas basadas en entropía tengan en cuenta todos los puntos de datos relevantes para evitar la exclusión de grupos marginados.
En IA, si bien la entropía cuantifica la incertidumbre, es nuestra responsabilidad garantizar que que la forma en que lo manejamos refleja un compromiso con la justicia y la inclusión. La creación de sistemas transparentes que prioricen la inclusión no solo mejora la equidad, sino que también mejora la solidez de los modelos de IA al exponerlos a una gama más amplia de escenarios.
Transparencia en la toma de decisiones basada en la entropía
A medida que los sistemas de IA dependen cada vez más de la entropía para guiar la toma de decisiones, mantener la transparencia se vuelve fundamental. Esto es particularmente cierto en aplicaciones sensibles como la atención médica y la toma de decisiones legales, donde hay mucho en juego.
Explicar cómo las métricas de entropía influyen en las predicciones o decisiones de los modelos es vital para generar confianza y garantizar la responsabilidad.
Por ejemplo, en la IA médica, la entropía se utiliza a menudo para medir la incertidumbre en las predicciones de diagnóstico. Al comunicar esta incertidumbre a los profesionales de la salud, estos sistemas permiten una toma de decisiones más informada, cerrando la brecha entre los resultados algorítmicos y la experiencia humana.
Ampliando el papel de la entropía en la IA
La IA cuántica representa una convergencia de la inteligencia artificial y la computación cuántica, y la entropía está en el corazón de esta intersección. Los investigadores están explorando cómo las métricas de entropía cuántica, como la entropía de von Neumann, pueden optimizar las redes neuronales cuánticas y otros sistemas híbridos.
Estos avances son prometedores para resolver problemas complejos en campos como la logística, el descubrimiento de fármacos y las comunicaciones seguras.
Por ejemplo, los sistemas de IA cuántica podrían aprovechar la entropía para modelar interacciones moleculares intrincadas con factores sin precedentes. precisión, acelerando los avances en el sector farmacéutico. Al combinar las fortalezas probabilísticas de los sistemas cuánticos con la adaptabilidad de la IA, la entropía continúa expandiendo su influencia en las tecnologías de vanguardia.
Integración en flujos de trabajo de IA
La entropía se integra cada vez más en cada etapa de los flujos de trabajo de la IA, desde el preprocesamiento de datos hasta la toma de decisiones en tiempo real. Sirve como métrica unificadora para cuantificar la incertidumbre, permitiendo que los sistemas se adapten dinámicamente a las condiciones cambiantes.
Esta integración garantiza que la IA siga siendo flexible, confiable y capaz de abordar los desafíos de entornos complejos.
Industrias que van desde vehículos autónomos hasta modelos financieros se benefician de enfoques basados en la entropía, que mejorar la precisión de la predicción, la velocidad de toma de decisiones y la adaptabilidad. Al incorporar la entropía en el núcleo del desarrollo de la IA, los investigadores están construyendo sistemas que no sólo son técnicamente sólidos sino que también están alineados con objetivos éticos y sociales.
Lo que nos espera
La entropía ha evolucionado de un concepto termodinámico a una piedra angular de la inteligencia artificial. Al cuantificar la incertidumbre, permite que los sistemas de IA equilibren la aleatoriedad y la estructura, fomentando la adaptabilidad, la creatividad y la precisión. Ya sea guiando algoritmos de aprendizaje automático, gestionando datos sintéticos o impulsando innovaciones en IA cuántica, podemos ver claramente cómo la entropía está remodelando la forma en que la inteligencia artificial aprende y se adapta.
A medida que la IA continúa creciendo en complejidad e impacto, la comprensión y La aplicación de la entropía será esencial para construir sistemas que no sólo sean más inteligentes sino también más justos, más transparentes y mejor equipados para navegar las incertidumbres del mundo real.

