A inteligência artificial depende da sua capacidade de interpretar dados, adaptar-se a ambientes dinâmicos e tomar decisões com informações incompletas. No centro desses processos está a entropia – uma métrica que quantifica a incerteza e a aleatoriedade.
Originalmente cconcebida na termodinâmica, a entropia agora desempenha um papel fundamental na IA, orientando sistemas para equilibrar estrutura com flexibilidade e melhorar sua capacidade de lidar com tarefas complexas.
Claude Shannon redefiniu a entropia em 1948, transformando-a em uma medida de incerteza para os sistemas de informação. O trabalho de Shannon forneceu uma estrutura matemática para otimizar a transmissão de dados, e seus insights estão agora incorporados em disciplinas de IA.
Hoje, a entropia impulsiona inovações em aprendizado de máquina, criação de dados sintéticos e modelos generativos , aprendizagem por reforço e computação quântica. À medida que a IA se torna mais integrante das tecnologias modernas, compreender as aplicações da entropia é fundamental para sistemas mais inteligentes e adaptáveis.
As Origens da Entropia
A entropia foi introduzida pela primeira vez no século 19, enquanto os cientistas procuravam compreender a eficiência energética em sistemas termodinâmicos. estudos pioneiros de Sadi Carnot sobre calor motores inspiraram Rudolf Clausius a definir entropia formalmente.
Clausius descreveu-o como a porção de energia num sistema que não pode ser convertida em trabalho, refletindo a tendência do universo para uma maior desordem. Este conceito termodinâmico lançou as bases para a compreensão da aleatoriedade e da irreversibilidade em sistemas físicos.
A descoberta de Claude Shannon
Claude Shannon revolucionou a entropia ao aplicá-la aos sistemas de informação. Em seu artigo seminal A Mathematical Theory of Communication, Shannon descreveu a entropia como um medida de incerteza em um conjunto de dados. Ele escreveu: “O problema fundamental da comunicação é reproduzir em um ponto exatamente ou aproximadamente uma mensagem selecionada em outro ponto.”
A entropia de Shannon quantificou a imprevisibilidade da informação, permitindo aos engenheiros calcular a eficiência da comunicação. transmissão e compressão de dados. Sua fórmula estabeleceu a entropia como uma métrica universal para medir a incerteza, vinculando-a a distribuições de probabilidade e criando uma base para tecnologias modernas baseadas em dados.
Entropia na Máquina. Aprendizado
No aprendizado de máquina, a entropia avalia a aleatoriedade ou impureza nos conjuntos de dados, orientando algoritmos para tomar decisões que minimizem a incerteza
Árvores de decisão, por exemplo, usam entropia para determinar as divisões mais informativas. Atributos que maximizam o ganho de informação, ou a redução na entropia, são escolhidos como critérios de divisão, melhorando a precisão da classificação do modelo.
Considere um conjunto de dados com rótulos de classes mistas: sua alta entropia reflete imprevisibilidade. Ao dividir os dados em subconjuntos baseados em um atributo específico, a entropia é reduzida, resultando em grupos mais homogêneos.
Este processo iterativo constrói uma árvore de decisão que reduz sistematicamente a incerteza, criando uma estrutura otimizada para previsões precisas.
A fórmula para ganho de informação é a seguinte:
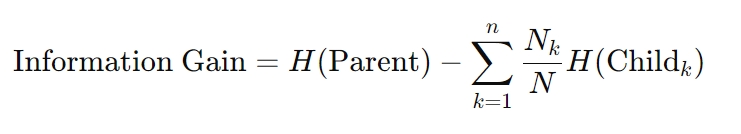
Aqui, H representa a entropia, Nk é a contagem de amostras no k-ésimo nó filho e N é o total contagem de amostras no nó pai. Este cálculo garante que cada decisão reduza ao máximo a incerteza, um princípio fundamental para algoritmos de árvore de decisão.
Perda de entropia cruzada em redes neurais
A entropia também sustenta a otimização técnicas em redes neurais. Perda de entropia cruzada, uma métrica amplamente utilizada em tarefas de classificação, mede a divergência entre probabilidades previstas e rótulos reais. Minimizar essa perda alinha as previsões de um modelo com os resultados do mundo real, melhorando a precisão.
A fórmula para perda de entropia cruzada é:
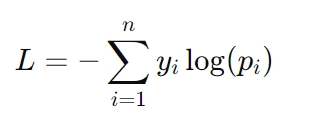
Aqui, yi representa o rótulo real (por exemplo, 0 ou 1) e pi é a probabilidade prevista para esse rótulo. A perda de entropia cruzada é especialmente crítica em tarefas como reconhecimento de imagem e modelagem de linguagem, onde previsões precisas de probabilidade são necessárias para o sucesso.
O papel da entropia na criação de dados sintéticos
Os dados sintéticos tornaram-se um recurso crítico no desenvolvimento de IA, oferecendo soluções para desafios como acesso limitado a conjuntos de dados do mundo real, preocupações com privacidade e restrições de custos.
No entanto, a eficácia dos conjuntos de dados sintéticos depende muito dos seus níveis de entropia. Os dados sintéticos de alta entropia introduzem a variabilidade necessária para imitar as condições do mundo real, permitindo que os modelos de IA generalizem melhor para novos cenários.
No entanto, a entropia excessiva pode introduzir ruído, levando a overfitting — onde o modelo fica excessivamente ajustado aos dados de treinamento e não consegue ter um bom desempenho em exemplos não vistos.
Em contraste, os conjuntos de dados de baixa entropia simplificam o aprendizado, mas podem subrepresentar a complexidade dos dados do mundo real. Este desequilíbrio corre o risco de underfitting, onde os modelos não conseguem capturar padrões significativos, resultando numa generalização deficiente. Encontrar o equilíbrio certo entre esses extremos é fundamental para criar dados sintéticos de alta qualidade.
Técnicas para otimizar dados sintéticos com entropia
Para enfrentar os desafios apresentados pela entropia em conjuntos de dados sintéticos, os pesquisadores empregam técnicas avançadas que melhoram a qualidade dos dados, mantendo a relevância:
Seleção de entropia com maximização de similaridade sintética real (ESRM): ESRM identifica amostras sintéticas que refletem de perto dados do mundo real, garantindo que os conjuntos de dados de treinamento permaneçam diversos, mas gerenciáveis. O equilíbrio da entropia em conjuntos de dados sintéticos garante que os modelos sejam treinados em exemplos diversos, porém relevantes, reduzindo o ruído e preservando a utilidade. Limpeza e normalização de dados: esses processos ajudam a eliminar a aleatoriedade excessiva, alinhando as distribuições de dados sintéticos com as dos conjuntos de dados do mundo real. A normalização garante que os conjuntos de dados sejam compatíveis com algoritmos de aprendizado de máquina, facilitando uma convergência de modelos mais suave. Seleção de recursos: ao focar em recursos ricos em entropia que fornecem os insights mais informativos, a seleção de recursos reduz a redundância e o ruído, tornando os dados sintéticos mais eficazes para o treinamento de modelos.
Esses métodos melhoram a confiabilidade dos dados sintéticos, ajudando os sistemas de IA a alcançar uma generalização robusta sem ajuste excessivo ou insuficiente.
IA generativa: criatividade e controle por meio da entropia
A IA generativa, que inclui sistemas como geradores de texto, criadores de imagens e ferramentas de síntese de áudio, depende da entropia para controlar o equilíbrio entre criatividade e coerência.
Ao ajustar os limites de entropia, os desenvolvedores podem influenciar o quão previsíveis ou variados são os resultados gerados.
Por exemplo, uma configuração de baixa entropia garante que as respostas sejam focadas e relevantes, ideal para aplicações como chatbots de atendimento ao cliente ou assistentes automatizados de redação. Por outro lado, uma entropia mais elevada introduz diversidade e novidade, permitindo tarefas criativas, como geração de arte ou narrativa.
Esse controle é fundamental para adaptar a IA generativa a casos de uso específicos. Em aplicações práticas, os ajustes de entropia ajudam a manter um equilíbrio entre inovação e precisão, garantindo que os resultados atendam aos objetivos desejados sem comprometer a qualidade.
Autenticação de conteúdo gerado por IA
A entropia também desempenha um papel vital na verificação da autenticidade do conteúdo gerado por IA. Estudos demonstraram que o texto gerado por IA tende a exibir menor entropia em comparação com o material escrito por humanos, tornando-o mais fácil de detectar.
Essa lacuna mensurável fornece uma referência para distinguir conteúdo sintético de expressões humanas autênticas.
Essas métricas têm aplicações práticas no combate à desinformação e na garantia da integridade do conteúdo gerado por IA. As organizações usam a análise de entropia para identificar o possível uso indevido de IA generativa em deepfakes, notícias falsas ou propaganda automatizada, destacando sua importância crescente na verificação de conteúdo.
Aprendizado por reforço: explorando o desconhecido com entropia
Em reforço aprendizagem (RL), a entropia é crítica para manter o delicado equilíbrio entre exploração e exploração. A exploração envolve tentar novas ações para descobrir melhores estratégias, enquanto a exploração se concentra em refinar ações conhecidas para maximizar as recompensas. Políticas de alta entropia incentivam a seleção diversificada de ações, evitando que os agentes fiquem presos em soluções abaixo do ideal.
Este princípio é especialmente valioso em ambientes dinâmicos, como robótica autônoma, IA de jogos e sistemas de logística adaptativos, onde flexibilidade e adaptabilidade são essenciais.
Regularização de entropia — uma técnica que introduz um termo de penalidade com base na entropia da política — garante que os agentes retenham aleatoriedade suficiente para explorar estratégias alternativas sem comprometer o desempenho a longo prazo.
Estabilizando a aprendizagem com entropia
Métodos de gradiente de política, uma classe de algoritmos RL, também se beneficiam dos efeitos estabilizadores da entropia. Ao manter a aleatoriedade controlada no processo de tomada de decisão do agente, a entropia evita a convergência prematura e promove uma exploração mais abrangente.
A entropia garante que os agentes de aprendizagem por reforço permaneçam adaptáveis, permitindo-lhes prosperar em ambientes complexos e imprevisíveis.
Entropia em computação quântica e compressão de dados
Na computação quântica, a entropia desempenha um papel crítico na avaliação da coerência e do emaranhamento da computação quântica. estados. Ao contrário dos sistemas clássicos, onde a entropia quantifica a desordem nas distribuições de dados, a entropia quântica captura a natureza probabilística dos sistemas quânticos.
Métricas como von entropia de Neumann são amplamente utilizadas para medir a incerteza e orientar a otimização de sistemas quânticos híbridos. algoritmos clássicos.
Esses algoritmos aproveitam a entropia quântica para resolver problemas que são computacionalmente inviáveis para sistemas clássicos, como tarefas complexas de otimização, criptografia e simulações de estruturas moleculares.
Por exemplo, a entropia de von Neumann é fundamental no refinamento das redes neurais quânticas, que combinam os princípios probabilísticos da mecânica quântica com estruturas tradicionais de aprendizado de máquina. A entropia basicamente une a incerteza inerente à mecânica quântica com a previsibilidade exigida pelos sistemas clássicos.
A entropia quântica também auxilia na correção de erros, um desafio importante na computação quântica. Ao identificar e minimizar fontes de entropia em sistemas quânticos, os desenvolvedores podem melhorar a estabilidade e a confiabilidade dos qubits, abrindo caminho para tecnologias quânticas mais robustas.
Compressão de dados baseada em entropia
A entropia sustenta algoritmos de compressão de dados, permitindo armazenamento e transmissão eficientes, reduzindo redundância, preservando informações essenciais. As técnicas de compactação analisam os níveis de entropia nos conjuntos de dados para otimizar os esquemas de codificação, alcançando um equilíbrio entre minimizar o tamanho dos arquivos e manter a integridade dos dados.
Essa abordagem é particularmente valiosa em ambientes com largura de banda restrita, como redes IoT e sistemas de computação de ponta.
Por exemplo, métodos de compactação baseados em entropia permitem que dispositivos IoT transmitam dados de sensores com mais eficiência, reduzindo o consumo de energia e o uso de largura de banda. Ao aproveitar a entropia como métrica orientadora, esses sistemas alcançam alto desempenho sem comprometer a precisão ou a confiabilidade.
Considerações Éticas: Inclusão, Preconceito e Transparência
Conjuntos de dados de alta entropia geralmente incluem exemplos diversos e menos comuns, como dados que representam grupos sub-representados. Estes pontos de dados são essenciais para a construção de sistemas de IA equitativos, mas podem ser excluídos inadvertidamente durante os processos de otimização da entropia, levando a resultados tendenciosos.
Os desenvolvedores devem garantir que as técnicas baseadas em entropia considerem todos os pontos de dados relevantes para evitar a exclusão de grupos marginalizados.
Na IA, embora a entropia quantifique a incerteza, é nossa responsabilidade garantir que a forma como lidamos com isso reflete um compromisso com a justiça e a inclusão. Construir sistemas transparentes que priorizem a inclusão não apenas melhora a justiça, mas também aumenta a robustez dos modelos de IA, expondo-os a uma gama mais ampla de cenários.
Transparência na tomada de decisões baseada na entropia
À medida que os sistemas de IA dependem cada vez mais da entropia para orientar a tomada de decisões, manter a transparência torna-se fundamental. Isto é particularmente verdadeiro em aplicações sensíveis, como cuidados de saúde e tomada de decisões jurídicas, onde os riscos são elevados.
Explicar como as métricas de entropia influenciam as previsões ou decisões do modelo é vital para construir confiança e garantir a responsabilidade.
Por exemplo, na IA médica, a entropia é frequentemente usada para medir a incerteza nas previsões de diagnóstico. Ao comunicar esta incerteza aos profissionais de saúde, estes sistemas permitem uma tomada de decisão mais informada, preenchendo a lacuna entre os resultados algorítmicos e a experiência humana.
Expandindo o papel da entropia na IA
A IA quântica representa uma convergência entre inteligência artificial e computação quântica, e a entropia está no centro dessa interseção. Os pesquisadores estão explorando como as métricas de entropia quântica, como a entropia de von Neumann, podem otimizar redes neurais quânticas e outros sistemas híbridos.
Esses avanços são promissores para a solução de problemas complexos em áreas como logística, descoberta de medicamentos e comunicações seguras.
Por exemplo, os sistemas de IA quântica poderiam aproveitar a entropia para modelar interações moleculares complexas com dados sem precedentes. precisão, acelerando avanços em produtos farmacêuticos. Ao combinar os pontos fortes probabilísticos dos sistemas quânticos com a adaptabilidade da IA, a entropia continua a expandir a sua influência em tecnologias de ponta.
Integração entre fluxos de trabalho de IA
A entropia está sendo cada vez mais integrada em todas as etapas dos fluxos de trabalho de IA, desde o pré-processamento de dados até a tomada de decisões em tempo real. Serve como uma métrica unificadora para quantificar a incerteza, permitindo que os sistemas se adaptem dinamicamente às mudanças nas condições.
Essa integração garante que a IA permaneça flexível, confiável e capaz de enfrentar os desafios de ambientes complexos.
Indústrias que vão desde veículos autônomos até modelagem financeira se beneficiam de abordagens baseadas na entropia, que aumentar a precisão das previsões, a velocidade da tomada de decisões e a adaptabilidade. Ao incorporar a entropia no núcleo do desenvolvimento da IA, os pesquisadores estão construindo sistemas que não são apenas tecnicamente robustos, mas também alinhados com objetivos éticos e sociais.
O que vem pela frente
A entropia evoluiu de um conceito termodinâmico para uma pedra angular da inteligência artificial. Ao quantificar a incerteza, permite que os sistemas de IA equilibrem a aleatoriedade e a estrutura, promovendo a adaptabilidade, a criatividade e a precisão. Seja orientando algoritmos de aprendizado de máquina, gerenciando dados sintéticos ou impulsionando inovações em IA quântica, podemos ver claramente como a entropia está remodelando a forma como a inteligência artificial aprende e se adapta.
À medida que a IA continua a crescer em complexidade e impacto, a compreensão e o impacto aplicar a entropia será essencial para construir sistemas que não sejam apenas mais inteligentes, mas também mais justos, mais transparentes e mais bem equipados para navegar nas incertezas do mundo real.